Teori Dasar Induktor
Induktor adalah komponen elektronika yang berfungsi untuk menghasilkan medan magnetik, tegangan induksi atau arus induksi. Induktor bekerja menurut hukum Faraday. Induktor tidak lain adalah lilitan kawat pada sebuah coker atau inti logam. Pada saat arus listrik (i) melewati lilitan kawat ini, maka akan timbul fluks magnetik (NΦ) di sekitar induktor yang besarnya proporsional dengan kuat arus listrik yang melewatinya. Gambar berikut ini menunjukan macam-macam induktor yang sering dijumpai dalam komponen elektronika.
Gambar 1 macam-macam jenis induktor yang ada dipasaran
Induktor sering disebut juga Choke. Simbol induktor sebagai berikut.
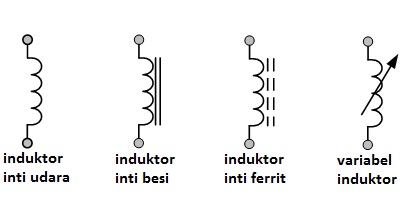 Gambar 2 macam-macam simbol induktor
Gambar 2 macam-macam simbol induktor
Induktor terbuat dari lilitan kawat pada sebuah inti. Konstruksi induktor dapat dilihat seperti pada gambar berikut ini.
Gambar 3 konstruksi sebuah induktor sederhana
Arus yang melewati sebuah induktor akan menghasilkan medan magnet yang besarnya berbanding lurus dengan arus listrik yang mengalir. Tidak seperti kapasitor yang terjadi perubahan kenaikan tegangan pada kedua lempeng konduktor ketika sedang diisi muatan listrik, pada konduktor justru timbul perubahan kenaikkan arus listrik ketika diberi tegangan listrik, perubahan kenaikan arus listrik ini menciptakan induksi energi di dalam medan magnet. Dengan kata lain induktor mengatur perubahan arus listrik dan dengan tidak mengubah tegangan listrik. Kemampuan induktor ini disebut induktansi induktor dengan satuan Henry (H) dan diberi simbol L. Untuk ukuran yang lebih kecil biasanya dinyatakan dalam satuan miliHenry (mH), mikroHenry (µH), nanoHenry (nH) dan picoHenry (pH).
Sebuah induktor mempunyai inti dengan luas penampang inti (A), Jumlah lilitan kawat per satuan panjang (l) . Jadi jika sebuah induktor dengan N lilitan kawat dihubungkan dengan sejumlah fluk magnetik (Φ) maka induktor akan mempunyai fluk magnetik total sebesar N.Φ. dan arus sebesar i yang mengalir melewatinya akan menghasilkan induksi fluk magnetik yang arahnya berlawanan dengan arah aliran arus listrik. Menurut hukum Faraday, semua perubahan fluk magnetik akan menghasilkan tegangan induksi yang besarnya :
Di mana : N adalah banyaknya lilitan, A adalah luas penampang inti (m2), Φ adalah fluks magnetik (Wb), µ adalah permeabilitas material inti, l adalah panjang induktor (m) dan (di/dt) adalah laju perubahan arus dalam satuan A/s.
Laju perubahan medan magnetik (dΦ/dt) yang menginduksi tegangan besarnya proporsional dengan laju perubahan arus listrik (di/dt) . atau dapat ditulis:
 dimana L adalah induktansi induktor yang besarnya :
dimana L adalah induktansi induktor yang besarnya :
Maka tegangan induksi sebuah induktor dapat ditulis :
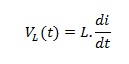
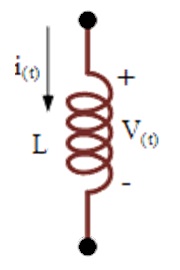 Gambar 4 tegangan induksi induktor
Gambar 4 tegangan induksi induktor
Dari persamaan ini dapat dikatakan emf induksi = induktansi x laju perubahan arus listrik. Sebuah rangkaian yang memiliki induktasi 1 Henry dengan tegangan induksi 1 Volt akan menghasilkan laju perubahan arus listrik sebesar 1 Ampere/detik.
Dari persamaan ini terlihat yang berubah hanya arus listrik, sedangkan tegangan induksi tidak berubah. Maka bila tegangan induksi = 0, perubahan arus listrik juga akan menjadi 0. Bila induktor dihubungkan dengan sumber arus DC arus listriknya konstan terhadap waktu, maka tidak akan timbul tegangan induksi pada induktor dan induktor hanya berfungsi sebagai sebuah penghantar saja.
Pada konduktor arus listrik tidak dapat berubah secara mendadak karena jika hal ini terjadi, maka akan dibutuhkan tegangan dan daya yang tidak terhingga besarnya (di/dt = ∼). Sebuah induktor dengan induktansi 1 H dengan arus maksimum 1 A , bila perubahan arus dari 0 hingga maksimum dalam waktu 1 detik, maka tegangan yg dibutuhkan akan sebesar 1 V dapat digambar seperti pada gambar berikut ini.
 Gambar 5 hubungan tegangan dan kuat arus pada induktor dengan dt=1 s dan di = 1 A
Gambar 5 hubungan tegangan dan kuat arus pada induktor dengan dt=1 s dan di = 1 A
Pada induktor yg sama , jika kita mengurangi dt hingga 1/10 nya atau perubahan arus sebesar 1 A dalam waktu 0,1 detik, maka tegangan yang dibutuhkan akan menjadi 10 kali lipat besarnya yaitu 10 V, dapat dilihat pada gambar berikut ini.
 Gambar 6 hubungan i dengan V bila dt diubah menjadi 0,1 detik
Gambar 6 hubungan i dengan V bila dt diubah menjadi 0,1 detik
Pada induktor yang sama, jika perubahan arus terjadi mendadak atau sangat cepat (dt=0) maka tegangan yang dibutuhkan menjadi tidak terhingga besarnya atau dapat digambar seperti pada gambar berikut ini.
 Gambar 7 bila dt=0 maka V akan menjadi tidak terhingga besarnya
Gambar 7 bila dt=0 maka V akan menjadi tidak terhingga besarnya
Daya di dalam induktor
Daya listrik secara matematis dapat ditulis :
P = V.i
Di mana P : daya listrik (Watt), V : tegangan listrik (V) dan i adalah arus listrik (A)
Pada induktor berlaku persamaan :
Maka daya induktor dapat ditulis :
Sebuah induktor ideal tidak mempunyai hambatan (R=0) sehingga tidak ada rugi-rugi daya di dalam induktor, jadi dapat dikatakan induktor ideal tidak terjadi rugi-rugi daya.
Ketika ada daya yang mengalir melalui sebuah induktor, maka energi listrik disimpan di dalam induktor dalam bentuk medan magnetik. Ketka arus listrik meningkat dalam selang waktu (dt) yang mendekati nol, maka daya sesaat di dalam rangkaian juga akan meningkat dan energi disimpan di dalam induktor. Sebaliknya jika arus yang mengalir melewati induktor berkurang maka daya sesaat juga akan turun (menjadi negatif). Ini berarti induktor akan membuang sejumlah energi dari rangkaian.
Energi disimpan dalam bentuk medan magnet yang timbul disekitar induktor. Pada induktor ideal, tidak terdapat hambatan atau kapasitansi, sehingga arus yang naik ketika melewati induktor akan disimpan dalam bentuk medan listrik tanpa ada rugi-rugi. Medan listrik ini tidak berkurang besarnya.
Bila induktor dilewatkan arus AC, maka induktor akan secara berkala menyimpan dan membuang energi dalam bentuk siklus. Pada arus DC arus yang melewati induktor besarnya konstan, maka tidak terjadi proses penyimpanan dan pembuangan energi secara berulang-ulang seperti pada arus AC.
Melihat cara kerja induktor, dapat disimpulkan bahwa induktor adalah komponen pasif elektronika yang dapat menyimpan dan menyalurkan energi listrik ke rangkaian listrik. Tetapi induktor tidak dapat membangkitkan energi listrik.
Pada induktor real terdapat kerugian daya listrik akibat adanya hambatan di dalam kawat penghantar induktor. Besar kerugian daya ini dapat dihitung dengan persamaan :
P =i2R
Di mana i adalah arus listrik (A), R hambatan dalam induktor (Ohm) dan P adalah kerugian daya listrik (W).
Fungsi utama induktor di dalam rangkaian listrik adalah sebagai filter, rangkaian resonansi dan sebagai pembatas arus listrik. Sebuah induktor dapat digunakan untuk memblock arus AC atau memblok frekuensi tertentu dari arus AC. Oleh sebab itu induktor dapat digunakan untuk menyaring frekuensi radio atau memfilter frekuensi yang melewatinya. Induktor juga dapat digunakan untuk menjaga perangkat elektronika dari kenaikan tegangan dan arus listrik yang mendadak.
Induksi Diri (Self Inductance) sebuah induktor
Induktor menghasilkan induksi dengan cara membangkitkan induksi emf (electro magnetic force) di dalam induktor itu sendiri akibat dari adanya perubahan medan magnet. Di dalam rangkaian elektronika, ketika terjadi induksi emf di dalam rangkaian, maka akan terjadi perubahan arus listrik yang disebut induksi diri, Induksi diri induktor sering disebut emf (tegangan) balik. Tegangan balik induktor ini memiliki arah yang berlawanan.
Induksi diri dapat ditulis secara matematik :
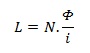 Di mana L adalah induksi diri (Henry), N : banyaknya lilitan, Φ : fluk medan magnet (Weber) dan i adalah kuat arus listrik (A). Persamaan ini berlaku hanya untuk induktor dengan 1 lapisan lilitan kawat.
Di mana L adalah induksi diri (Henry), N : banyaknya lilitan, Φ : fluk medan magnet (Weber) dan i adalah kuat arus listrik (A). Persamaan ini berlaku hanya untuk induktor dengan 1 lapisan lilitan kawat.
Fluk medan magnet adalah kerapatan medan magnet yang dapat dinyatakan :
Φ = B.A
Di mana : Φ adalah fluks medan magnet (Weber) , B adalah kuat medan magnet (Tesla) dan A adalah luas penampang yang dilewati oleh medan magnet (m2).
Maka induktansi sebuah induktor dapat ditulis ulang menjadi :
Untuk induktor dengan inti udara, kuat medan magnet dapat dinyatakan dengan persamaan :
Dengan N adalah banyaknya lilitan, i : arus listrik yang mengalir, l : panjang lilitan dan µ0 adalah permeabilitas ruang kosong (4π x 10-7). Maka persamaan induktansi induktor dapat ditulis menjadi :
Di mana : L adalah induktansi induktor (Henry); µ0 adalah permeabilitas ruang hampa (4π x 10-7); N adalah banyaknya lilitan, A adalah luas penampang induktor (m2) dan l adalah panjang lilitan (m).
Jadi induktansi sebuah induktor berbanding kuadratik terhadap jumlah lilitan dan luas penampang induktor, tetapi berbanding terbalik dengan panjang lilitan induktor. Untuk meningkatkan induktansi induktor dapat dilakukan dengan mengganti inti udara dengan inti logam.
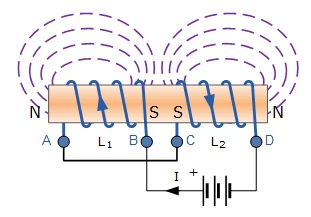
Induksi antara 2 induktor
 Gambar 8 dua buah induktor yang saling berdekatan
Gambar 8 dua buah induktor yang saling berdekatan
Gambar 8 menunjukan 2 buah induktor yang saling berdekatan. Induktor 1 dihubungkan dengan arus listrik AC maka pada induktor 1 akan timbul fluks medan magnet. Akibatnya pada induktor 2 akan terinduksi oleh medan magnet sehingga timbul tegangan dan arus listrik. Prinsip ini disebut mutual induksi. Besar Mutual induksi ini dapat dihitung dengan persamaan :
Di mana µ0 adalah permeabilitas udara yang memisahkan kedua induktor, µr permeabilitas bahan inti induktor, N1 dan N2 adalah jumlah lilitan induktor 1 dan induktor 2, A luas penampang induktor dalam hal ini kedua induktor memiliki luas penampang yang sama dan l adalah panjang induktor.
 Gambar 9 dua buah induktor yang dipasang pada satu buah inti besi
Gambar 9 dua buah induktor yang dipasang pada satu buah inti besi
Mutual induksi untuk induktor 2 terhadap induktor 1 yang dipasang pada satu inti seperti pada gambar 9 adalah
Di mana l1 adalah panjang induktor 1, N2 adalah banyaknya lilitan pada induktor 2
Sebaliknya mutal induksi untuk induktor 1 terhadap induktor 2 adalah :
Besar kedua mutual induksi ini sama sehingga dapat ditulis M12 = M21 = M
Induktansi kedua induktor adalah :
Dengan perkalian silang didapat :
Persamaan ini menyatakan tidak ada kebocoran / kehilangan fluks magnetik. Namun dalam kenyataannya fluk magnetik pasti ada yang hilang. Sehingga persamaan mutual induksi yang sebenarnya dengan mempertimbangkan kerugiaan fluk magnetik dapat ditulis :
Di mana k adalah koefisien penghubung (coupling coefficient) . jika k = 1 maka tidak ada kerugian fluk magnetik, pada kenyataannya k selalu < 1.
Induktor seri dan paralel.
Induktor yang dirangkai seri
Selain kapasitor dan resistor, induktor juga dapat dirangkai secara seri. Induktor yang dipasang seri maka induktansinya dapat dihitung sebagai berikut :
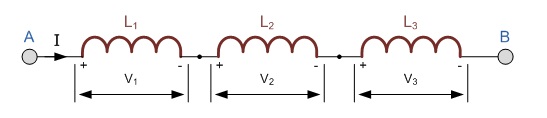 Gambar 10 induktor yang dipasang seri
Gambar 10 induktor yang dipasang seri
Sama seperti resistor bila induktor dirangkai secara seri, maka tidak terjadi pembagian arus listrik, karena tidak terdapat percabangan. Sehingga dapat ditulis :
iL1 = iL2 = iL3
Tetapi terjadi pembagian tegangan dan total tegangan pada induktor dapat ditulis :
VT = VL1 + VL2 + VL3
Untuk induktor tegangan dapat dinyatakan :
Mutual induksi yang dihasilkan oleh induktor yang dirangkaian seri dapat dibagi menjadi 2 yaitu kumulatif kopel dan diferensial kopel. Kumulatif kopel dapat dilihat seperti pada gambar berikut ini.
Gambar 11 kumulatif kopel pada induktor seri
Besar mutual induksi pada kumulatif kopel dapat dihitung :
Diferensial kopel dapat dilihat seperti pada gambar berikut ini.
 Gambar 12 diferensial kopel pada induktor seri
Gambar 12 diferensial kopel pada induktor seri
Besar mutual induksi dapat dihitung :
Secara garis besar induktor yang dirangkai secara seri bila diketahui mutual induksinya dapat dihitung dengan persamaan
LT = L1 + L2 + L3 ± 2M
Induktor yang dirangkai paralel
Rangkain induktor paralel dapat dilihat seperti pada gambar berikut ini.
 Gambar 13 induktor yang dirangkai secara paralel
Gambar 13 induktor yang dirangkai secara paralel
Induktor yang dirangkai secara paralel, maka tegangan tiap induktor akan sama tetapi terjadi pembagian arus listrik. Sehingga dapat ditulis :
VAB = VL1 = VL2 = VL3
dan
iT = iL1 + iL2 + iL3
Tegangan induktor adalah :
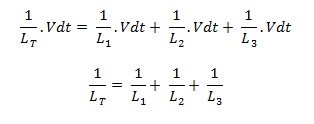 Mutual induksi pada rangkaian 2 induktor paralel dapat dibedakan menjadi 2 macam yaitu
Mutual induksi pada rangkaian 2 induktor paralel dapat dibedakan menjadi 2 macam yaitu
Rangkaian 2 induktor dengan arah lilitan yang sama yang besar induktansi totalnya dapat dihitung :
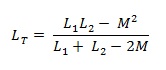 Jika kedua induktor yang diparalelkan berbeda arah lilitan, maka persamaan induktor total dapat dihitung :
Jika kedua induktor yang diparalelkan berbeda arah lilitan, maka persamaan induktor total dapat dihitung :
Rangkaian Induktor dan Resistor Seri (RL Circuit)
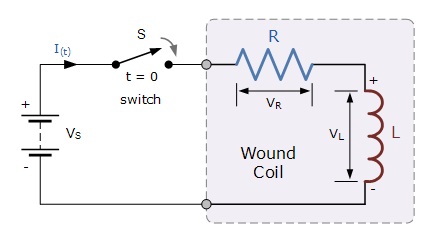
Sebuah rangkaian seri induktor dengan resistor dapat dilihat seperti pada gambar 15. Bila rangkaian ini dihubungkan dengan sumber arus DC yang dilengkapi dengan saklar, ketika saklar ditutup, maka arus akan mengalir melewati resistor dan ke induktor. Arus yang melewati resistor akan mengikuti persamaan hukum Ohm, sedangkan arus yang melewati induktor akan mengikuti hubungan tegangan dan arus listrik pada induktor.
Tegangan pada resistor dapat dihitung :
VR = i.R
Tegangan pada induktor dapat dihitung :
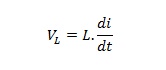 Maka tegangan total akan menjadi:
Maka tegangan total akan menjadi:
Penyelesaian persamaan diatas akan menjadi :
Jadi di dapat
Bandingkan dengan kapasitor !
Kurva i terhadap t dapat digambar seperti pada gambar 16 berikut ini.
 Gambar 15 kurva karakteristik induktor (*sumber : http://www.electronics-tutorials.ws)
Gambar 15 kurva karakteristik induktor (*sumber : http://www.electronics-tutorials.ws)
Daya dalam rangkaian seri induktor dengan resistor merupakan penjumlahan daya resistor dengan daya induktor atau secara matematik dapat ditulis :
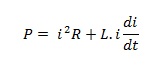 Di mana i2R adalah daya yang diserap oleh resistor daya ini diubah oleh resistor menjadi panas. Sedangkan L.i.(di/dt) adalah daya yang diserap oleh induktor dan disimpan dalam bentuk energi medan magnetik.
Di mana i2R adalah daya yang diserap oleh resistor daya ini diubah oleh resistor menjadi panas. Sedangkan L.i.(di/dt) adalah daya yang diserap oleh induktor dan disimpan dalam bentuk energi medan magnetik.
Terima kasih untuk http://www.electronics-tutorials.ws, karena beberapa gambar dan teori diambil dari web tersebut.
semoga berguna
Posted on Oktober 24, 2014, in Elektronika and tagged induksi, induktansi, Induktor, magnetik. Bookmark the permalink. 10 Komentar.





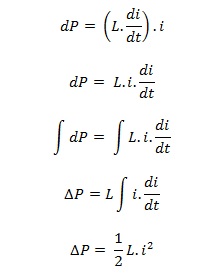
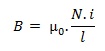
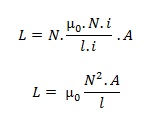
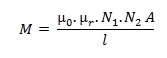
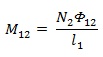
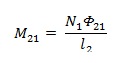
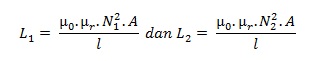
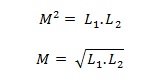
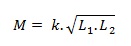
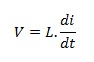
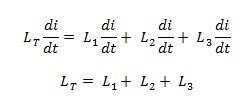

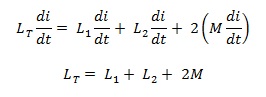
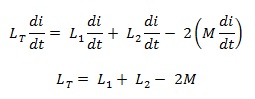
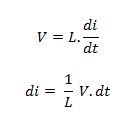
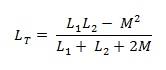
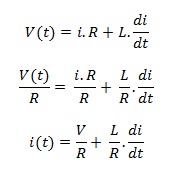
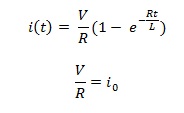
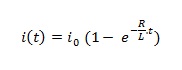
ijin share bapak,..
silakan, tolong dicek ulang, kalau ada salah diperbaiki
Maaf Pak, kalau tegangan pada kapasitor bagaimana ya?
Maksudnya tegangan kapasitor yang mana?. mungkin ini link bagus untuk belajar RLC circuit https://en.wikipedia.org/wiki/RLC_circuit
sangat membantu sekali pak, terimakasih
Trimakasih ilmunya master,,,,sangat bermanfaat buat saya….
sama-sama
Trimakasih atas ilmunya master,,saya sangat terbantu sekali…
dicek ulang lagi, kalau ada yg keliru diperbaiki
Ping-balik: Teori Dasar Induktor | La Tahzan..!